An intense focused laser pulse propagating in underdense plasma generates a plasma electron density wave behind it. The resulting plasma wave that is called laser wakefield supports high electric fields, and electrons can be accelerated to high energies in these fields within a very short length. The advantage of a laser wakefield accelerator is that plasmas support much higher electric fields compared to conventional accelerators.
When an ultra short relativistic intense focused laser pulse drives a plasma wave, the ponderomotive force of the laser expels all of the electrons transversely, and forms a region completely devoid of electrons behind the driving laser pulse. Plasma electrons can then be injected into this plasma "bubble", and become accelerated to multi-GeV.
Our research focuses on the bubble regime of laser wakefield accelerators, including the dynamics of self-injection, electron acceleration and dynamics inside of the bubble. Specially, we study self-injection both analytically and numerically. We have published papers on this process, focusing on non-stationary Hamiltonian models and particle-in-cell simulations.
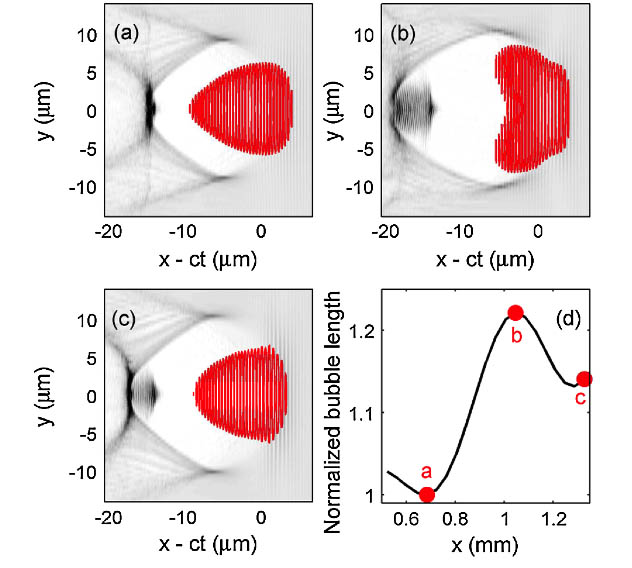
Figure 1. Electron self-injection [5]. Plasma bubble expands and contracts with the diffraction and focusing of laser pulse. Electrons are self-injected when plasma bubble expands.
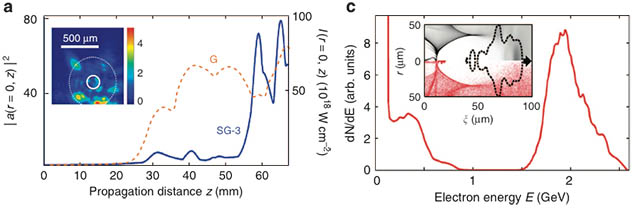
Figure 2. Laser self-focusing and 2 GeV electrons [1]. Self-focusing behavior is quite different between super-Gaussian and Gaussian laser pulse. Fast self-focusing and diffraction of super-Gaussian laser pulse get electrons self-injected and accelerated to 2 GeV.
Selected publications:
[1] Xiaoming Wang, Rafal Zgadzaj, Neil Fazel, Zhengyan Li, S. A. Yi, Xi Zhang, Watson Henderson, Y.-Y. Chang, R. Korzekwa, H.-E. Tsai, C.-H. Pai, H. Quevedo, G. Dyer, E. Gaul, M. Martinez, A. C. Bernstein, T. Borger, M. Spinks, M. Donovan, V. Khudik, G. Shvets, T. Ditmire & M. C. Downer, "Quasi-monoenergetic laser-plasma acceleration of electrons to 2 GeV," Nature Commun. 4:1988, doi: 10.1038/ncomms2988 (2013)
[2] S. A. Yi, V. Khudik, C. Siemon, and G. Shvets , "Analytic model of electromagnetic fields around a plasma bubble in the blow-out regime," Phys. Plasma. 20, 013108 (2013)
[3] S. A. Yi, V. Khudik, S. Kalmykov and G. Shvets, "Hamiltonian analysis of electron self-injection and acceleration into an evolving plasma bubble," Plasma Phys. Contr. Fus. 53, 014012 (2011).
[4] P. Dong, S. A. Reed, S. A. Yi, S. Kalmykov, G. Shvets, M. C. Downer, N. H. Matlis, W. P. Leemans, C. McGuffey, S. S. Bulanov, V. Chvykov, G. Kalintchenko, K. Krushelnick, A. Maksimchuk, T. Matsuoka, A. G. R. Thomas, and V. Yanovsky, "Formation of Optical Bullets in Laser-Driven Plasma Bubble Accelerators," Phys. Rev. Lett. 104, 134801 (2010).
[5] S. Kalmykov, S. A. Yi, V. Khudik and G. Shvets, "Electron Self-Injection and Trapping into an Expanding Plasma Bubble," Phys. Rev. Lett. 103, 135004 (2009).
[6] N. H. Matlis, S. Reed, S. S. Bulanov, V. Chvykov, G. Kalinitchenko, T. Matsuoka, P. Rousseau, V. Yanovsky, A. Maksimchuk, S. Kalmykov, G. Shvets, and M.C. Downer, "Snapshots of laser wakefields," Nature Phys. 2, 749 (2006).
[7] S. Yu. Kalmykov, L. M. Gorbunov, P. Mora, G. Shvets, "Injection, trapping, and acceleration of electrons in a three-dimensional nonlinear laser wakefield," Phys. Plasmas 13, 113102 (2006).
